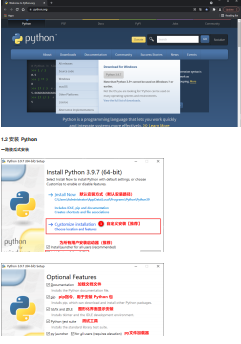
《矩阵分析(第3版)》是作者史荣昌、魏丰根据20多年教学实践经历3个版使用编写而成,主要介绍线性空间和线性变换,λ-矩阵与矩阵的Jordan标准形,矩阵的有理标准形,内积空间、正规矩阵、Hermite矩阵,矩阵分解,范数、序列、级数,矩阵函数,函数矩阵与矩阵微分方程,矩阵广义逆,Kronecker积。书适合高等院校学生、工学硕士、工程硕士研究生应用。...
目录
- 章线性空间和线性变换
- 1.1线性空间
- 1.2基与坐标、坐标变换
- 1.3线性子空间
- 1.4线性映射
- 1.5线性映射的值域、核
- 1.6线性变换的矩阵与线性变换的运算
- 1.7n维线性空间的同构
- 1.8线性变换的特征值与特征向量
- 1.9线性变换的不变子空间
- 1.10矩阵的相似对角形
- 习题
- 第二章λ-矩阵与矩阵的Jordan标准形
- 2.1λ-矩阵及标准形
- 2.2初等因子与相似条件
- 2.3矩阵的Jordan标准形
- 2.4矩阵的有理标准形
- 习题
- 第三章内积空间、正规矩阵、Hermite矩阵
- 3.1欧氏空问、酉空间
- 3.2标准正交基、Schmidt方法
- 3.3酉变换、正交变换
- 3.4幂等矩阵、正交投影
- 3.5对称与反对称变换
- 3.6Schur引理、正规矩阵
- 3.7Hermite变换、正规变换
- 3.8Hermite矩阵、Hermite二次齐式
- 3.9正定二次齐式、正定Hermite矩阵
- 3.10Hermite矩阵偶在复相合下的标准形
- 3.11Rayleigh商
- 习题
- 第四章矩阵分解
- 4.1矩阵的满秩分解
- 4.2矩阵的正交三角分解(UR、QR分解)
- 4.3矩阵的奇异值分解
- 4.4矩阵的极分解
- 4.5矩阵的谱分解
- 习题
- 第五章范数、序列、级数
- 5.1向量范数
- 5.2矩阵范数
- 5.3诱导范数(算子范数)
- 5.4矩阵序列与极限
- 5.5矩阵幂级数
- 5.6矩阵的测度
- 习题
- 第六章矩阵函数
- 6.1矩阵多项式、多项式
- 6.2矩阵函数及其Jordan表示
- 6.3矩阵函数的内插多项式表示与多项式表示
- 6.4矩阵函数的幂级数表示
- 6.5矩阵指数函数与矩阵三角函数
- 习题
- 第七章函数矩阵与矩阵微分方程
- 7.1函数矩阵对纯量的导数与积分
- 7.2函数向量的线性相关性
- 7.3矩阵微分方程
- 7.4线性向量微分方程
- 习题
- 第八章矩阵的广义逆
- 8.1广义逆矩阵
- 8.2伪逆矩阵
- 8.3广义逆与线...