我们帮大家精选了Python相关的编程文章,网友郝绍辉根据主题投稿了本篇教程内容,涉及到实验物理、python、python计算物理、python物理引擎、利用python求解物理学中的双弹簧质能系统详解相关内容,已被328网友关注,相关难点技巧可以阅读下方的电子资料。
利用python求解物理学中的双弹簧质能系统详解
前言
本文主要给大家介绍了关于利用python求解物理学中双弹簧质能系统的相关内容,分享出来供大家参考学习,下面话不多说了,来一起看看详细的介绍吧。
物理的模型如下:
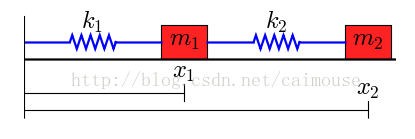
在这个系统里有两个物体,它们的质量分别是m1和m2,被两个弹簧连接在一起,伸缩系统为k1和k2,左端固定。假定没有外力时,两个弹簧的长度为L1和L2。
由于两物体有重力,那么在平面上形成摩擦力,那么摩擦系数分别为b1和b2。所以可以把微分方程写成这样:
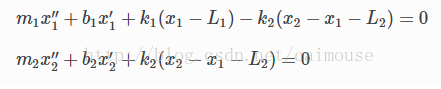
这是一个二阶的微分方程,为了使用python来求解,需要把它转换为一阶微分方程。所以引入下面两个变量:

这两个相当于运动的速度。通过运算可以改为这样:
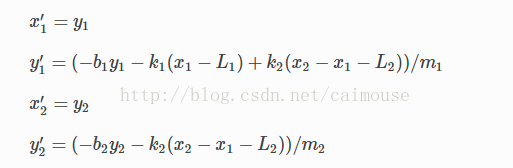
这时可以线性方程改为向量数组的方式,就可以使用python定义了
代码如下:
# Use ODEINT to solve the differential equations defined by the vector field
from scipy.integrate import odeint
def vectorfield(w, t, p):
"""
Defines the differential equations for the coupled spring-mass system.
Arguments:
w : vector of the state variables:
w = [x1,y1,x2,y2]
t : time
p : vector of the parameters:
p = [m1,m2,k1,k2,L1,L2,b1,b2]
"""
x1, y1, x2, y2 = w
m1, m2, k1, k2, L1, L2, b1, b2 = p
# Create f = (x1',y1',x2',y2'):
f = [y1,
(-b1 * y1 - k1 * (x1 - L1) + k2 * (x2 - x1 - L2)) / m1,
y2,
(-b2 * y2 - k2 * (x2 - x1 - L2)) / m2]
return f
# Parameter values
# Masses:
m1 = 1.0
m2 = 1.5
# Spring constants
k1 = 8.0
k2 = 40.0
# Natural lengths
L1 = 0.5
L2 = 1.0
# Friction coefficients
b1 = 0.8
b2 = 0.5
# Initial conditions
# x1 and x2 are the initial displacements; y1 and y2 are the initial velocities
x1 = 0.5
y1 = 0.0
x2 = 2.25
y2 = 0.0
# ODE solver parameters
abserr = 1.0e-8
relerr = 1.0e-6
stoptime = 10.0
numpoints = 250
# Create the time samples for the output of the ODE solver.
# I use a large number of points, only because I want to make
# a plot of the solution that looks nice.
t = [stoptime * float(i) / (numpoints - 1) for i in range(numpoints)]
# Pack up the parameters and initial conditions:
p = [m1, m2, k1, k2, L1, L2, b1, b2]
w0 = [x1, y1, x2, y2]
# Call the ODE solver.
wsol = odeint(vectorfield, w0, t, args=(p,),
atol=abserr, rtol=relerr)
with open('two_springs.dat', 'w') as f:
# Print & save the solution.
for t1, w1 in zip(t, wsol):
out = '{0} {1} {2} {3} {4}\n'.format(t1, w1[0], w1[1], w1[2], w1[3]);
print(out)
f.write(out);
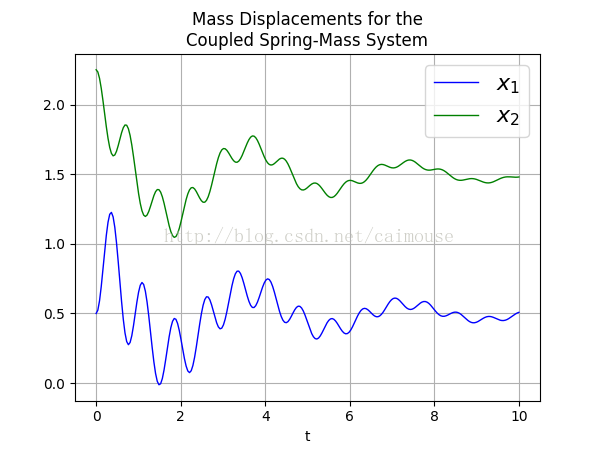
在这里把结果输出到文件two_springs.dat,接着写一个程序来把数据显示成图片,就可以发表论文了,代码如下:
# Plot the solution that was generated
from numpy import loadtxt
from pylab import figure, plot, xlabel, grid, hold, legend, title, savefig
from matplotlib.font_manager import FontProperties
t, x1, xy, x2, y2 = loadtxt('two_springs.dat', unpack=True)
figure(1, figsize=(6, 4.5))
xlabel('t')
grid(True)
lw = 1
plot(t, x1, 'b', linewidth=lw)
plot(t, x2, 'g', linewidth=lw)
legend((r'$x_1$', r'$x_2$'), prop=FontProperties(size=16))
title('Mass Displacements for the\nCoupled Spring-Mass System')
savefig('two_springs.png', dpi=100)
最后来查看一下输出的png图片如下:
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,如果有疑问大家可以留言交流,谢谢大家对码农之家的支持。